Membuat grafik fungsi kuadrat

Grafik fungsi kuadrat dalam matematika ditandai dengan f(x) = y yang merupakan variable terikat, x adalah variable bebas, sedangkan a, dan b merupakan koefisien dengan dinamakan persamaan kuadrat, yang mana persamaan kudarat, memiliki variable dengan pangkat tertingginya adalah dua dan berbentuk persamaan. Bentuk umum dari persamaan kuadrat yakni: dengan x adalah variable bebas, a dan b adalah koefisien, serta c adalah konstanta. Suatu fungsi sangat erat hubungannyan dengan grafik fungsi. Begitu pula fungsi kuadrat, yang memiliki grafik fungsinya sendiri.

Bentuk umum dari fungsi kuadrat yaitu f(x) = ax2 + bx + c, dengan keterangan sebagai berikut.

Keterangan:

a = koefisien dari x2, di mana a ≠ 0

b = koefisien dari x

c = konstanta

Ciri-Ciri Grafik Fungsi Kuadrat

Berikut ini terdapat beberapa ciri-ciri grafik fungsi kuadrat, antara lain:

1. Berbentuk parabola

2. Grafiknya simetris

3. Hanya memiliki titik maksimum saja atau titik minimum saja, namun tidak keduanya

Cara Merumuskan Fungsi Kuadrat Berdasarkan Grafik

Sebelum merumuskan fungsi kuadrat berdasarkan grafik, kita harus lihat dulu nih, nilai apa yang diketahui pada grafik tersebut, karena rumus yang akan kita pakai tergantung dari nilai apa yang diketahui pada grafik.

Contoh Soal Grafik Fungsi Kuadrat

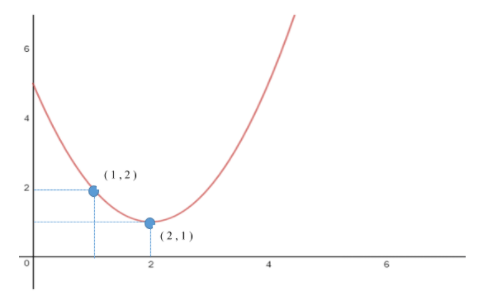
Dari grafik tersebut, diketahui titik puncak atau titik balik dari suatu fungsi kuadrat, yaitu di titik (2, 1). Selain itu, diketahui juga 1 titik sembarang yaitu (1, 2). Coba rumuskan fungsi kuadratnya!

Jawaban:

Diketahui dari soal bahwa:

(xp, yp) = (2, 1)
Titik sembarang = (1, 2)

Jika pada grafik diketahui titik puncak (xp, yp) dan 1 titik sembarang, maka kita menggunakan rumus:

y = a(x – xp)2 + yp

2 = a(1 – 2)2 + 1

2 = a(-1)2 + 1

2 = a(1) + 1

2 = a + 1

a = 2 – 1

a = 1

Karena titik puncaknya di (2, 1) dan nilai a = 1, maka fungsi kuadratnya:

y = a(x – xp)2 + yp

y = 1(x – 2)2 + 1

y = x2 – 4x + 4 + 1

y = x2 – 4x + 5

Jadi, dari grafik tersebut dapat kita rumuskan bahwa fungsi kuadratnya adalah

f(x) = x2 – 4x + 5.

2. Gambarlah grafik fungsi kuadrat f(x) = x² + 2x – 3

Jawab:

f(x) = x² + 2x – 3 memiliki a = 1; b = 2; c = -3

kita ikuti langkah-langkah di atas ya:

Langkah pertama: Tentukan titik potong dengan sumbu X (y = 0)

f(x) = x² + 2x – 3

x² + 2x – 3 = 0

Selanjutnya kita faktorkan, masih ingat pemfaktoran kan? Kalau lupa silahkan di refresh ingatan kalian disini.

jadi faktornya: (x + 3) (x – 1) = 0

a) titik 1:

x + 3 = 0

x = -3 karena y nya 0, maka titiknya (-3, 0) ..... titik (A)

b) titik 2

x – 1 = 0

x = 1 karena y nya 0, maka titiknya (1, 0) ..... titik (B)

Langkah kedua: Tentukan titik potong dengan sumbu Y (x = 0)

f(x) = x² + 2x – 3

y = x² + 2x – 3

y = (0)² + 2(0) – 3

y = -3 karena x = 0, maka titiknya (0, -3) .... titik (C)

Langkah ketiga: Tentukan titik balik atau titik puncak parabola

X = -1 maka y bernilai:

f(x) = x² + 2x – 3

y = x² + 2x – 3

y = (-1)² + 2(-1) – 3

y = 1 – 2 – 3

y = -4 maka titiknya adalah (-1, -4) .... titik (D)

Langkah keempat: Tentukan persamaan sumbu simetri.

Sekarang, kita gambar titik (A) – (D) (yang berwarna merah) pada bidang cartesius.

3. Matematika Dasar Fungsi Kuadrat (*Soal Dari Berbagai Sumber)

Persamaan grafik pada gambar adalah...
$\begin{aligned} (A) & y = x^{2} - 2 x + 2 \\ (B) & y = x^{2} + 2 x + 1 \\ (C) & y = x^{2} - 2 x + 1 \\ (D) & y = x^{2} - 2 x \\ (E) & y = x^{2} + 2 x \end{aligned}$

Dari gambar kita ketahui titik puncak parabola yaitu $(1, 1)$ dan melalui titik $(0, 2)$ . Dari unsur-unsur yang diketahui kita gunakan "Jika diketahui Titik Puncak $(x_{p}, y_{p})$ dan sebuah titik sembarang $(x, y)$ maka Fungsi Kuadrat adalah $y = a {(x - x_{p})}^{2} + y_{p}$ "

Untuk membentuk Fungsi Kuadrat terlebih dahulu kita cari nilai $a$ .
Pertama substitusi titik puncak $(1, 1)$ :
$y = a {(x - 1)}^{2} + 1$

Kedua substitusi titik sembarang $(0, 2)$ :
$\begin{aligned} 2 & = a {(0 - 1)}^{2} + 1 \\ 2 & = a {(- 1)}^{2} + 1 \\ 2 & = a + 1 \\ 1 & = a \end{aligned}$

Setelah diperoleh nilai $a = 1$ , fungsi kita kembalikan pada langkah pertama;
$\begin{aligned} y & = a {(x - 1)}^{2} + 1 \\ y & = {(x - 1)}^{2} + 1 \\ y & = x^{2} - 2 x + 1 + 1 \\ y & = x^{2} - 2 x + 2 \end{aligned}$

$∴$ Pilihan yang sesuai adalah $(A) y = x^{2} - 2 x + 2$

Muhammad Prayoga Ramadhani